نموذج الربو والخوف

25 1
الفترة رقم 1 : 0:00
سؤال رقم ( 1 )

كلب يلاحق أرنب و الفرق بينهم ١٥٠ قدم .. إذا كان الكلب يقفز ٩ق/ث و الأرنب يقفز ٧ق/ث كم عدد القفزات حتى يلحق به ؟

٧٥

١٥٠

٦٣

٢١٣

شرح الحل

الحل : أ

right to left زمن space اللحاق space equals space fraction numerator المسافة over denominator الفرق space بين space السرعتين end fraction space equals space fraction numerator 150 over denominator 9 space minus space 7 end fraction space equals space 150 over 2 space equals space 75 space space

الفترة رقم 1 : 0:00
سؤال رقم ( 2 )

right to left 9 to the power of س over 2 end exponent space equals space 81 space قارن بين:  س٢    و ٦

القيمة الأولى أكبر

القيمة الثانية أكبر

القيمتان متساويتان

المعطيات غير كافية

شرح الحل

الحل : (أ).

تتحقق المعادلة عندما س = ٤

 إذاً س٢ = ٢٤ = ١٦

الفترة رقم 1 : 0:00
سؤال رقم ( 3 )

ف = right to left 9 over 5 س + ٣٢ فإن س = ؟

right to left 5 over 9 (ف - ٣٢)

right to left 9 over 5 (ف - ٣٢)

right to left 5 over 9 (ف + ٣٢)

right to left 5 over 9 (٣٢ - ف)

شرح الحل

الحل : (أ).

نحل المعادلة بالنسبة لـ س :

ف - ٣٢ = right to left 9 over 5 س

"بالضرب ×right to left 5 over 9  "

س =right to left 5 over 9 (ف - ٣٢)

الفترة رقم 1 : 0:00
سؤال رقم ( 4 )

إذا كان الشكل التالي سداسي مساحته = ٤٢ سم٢ ، وكان س ن = ٣سم ، فأوجد س د

٢

٣

٤

٥

شرح الحل

الحل : أ

نكمل الشكل ليكون مستطيل كما هو موضح :

تكون مساحة المستطيل = ٦ × ٨ = ٤٨

نلاحظ أن

مساحة السداسي = مساحة المستطيل – الجزء المظلل

٤٢ = ٤٨ – س

س = ٦ سم٢

مساحة المظلل = ٦ سم٢

طوله = ٣ ، إذا لابد أن يكون العرض = ٢

الفترة رقم 1 : 0:00
سؤال رقم ( 5 )

كم عدد المكعبات في الشكل

١٣

١٤

٣٢

١١

شرح الحل

الاجابة : ب

الفترة رقم 1 : 0:00
سؤال رقم ( 6 )

إذا تم تحويل ١٠٠ ريال الى ٩٨ درهم فكم تحتاج من الريالات لتكوين ٤٩٠ درهم ؟

٣٠٠

٤٥٠

٥٠٠

٦٠٠

شرح الحل

الحل : (ج).

١٠٠ ----- ٩٨

  س ----- ٤٩٠

س = right to left fraction numerator 100 space cross times space 490 over denominator 98 end fraction = ٥٠٠

الفترة رقم 1 : 0:00
سؤال رقم ( 7 )

محطة تمتلك ٤ مولدات متساوية القدرة وتنتج ٥٠٠٠ واط ، فإذا تعطل مولد كم ستنتج ؟

٣٥٠٠

١٥٦٧

٤٠٠٠

٣٧٥٠

شرح الحل

الحل : (د).

بالتناسب الطردي

٤ ------  ٥٠٠٠

٣ ------  س

٤س = ٣ × ٥٠٠٠

س = ٣٧٥٠

الفترة رقم 1 : 0:00
سؤال رقم ( 8 )

أوجد قيمة الجزء المظلل إذا قسمنا نصف الدائرة إلى ٦ أقسام متساوية ؟

٥٠

٦٠

٣٠

٤٥

شرح الحل

الحل : (ج).

الدائرة بها ٣٦٠ درجة , نصفها = ١٨٠ درجة

فقيمة الجزء المظلل

١٨٠ ÷ ٦ = ٣٠°

الفترة رقم 1 : 0:00
سؤال رقم ( 9 )

س٢ - ٢س + ١ = ٠   ، قارن بين:  س    و   ١

القيمة الأولى أكبر

القيمة الثانية أكبر


القيمتان متساويتان

المعطيات غير كافية

شرح الحل

الحل : (ج).

بتحليل المعادلة :

(س -١) (س - ١) = ٠

س = ١

الفترة رقم 1 : 0:00
سؤال رقم ( 10 )

الزاوية أ = ٣٢° فأوجد الزاوية ج؟

١١٠

٥٨

٥٤

٦٤

شرح الحل

الحل : (ب).

الزواية ب = ٩٠°

الزاوية ج = ١٨٠ – (٩٠ + ٣٢) = ٥٨°

الفترة رقم 1 : 0:00
سؤال رقم ( 11 )

إذا كانت س أكبر من ص ، و ص أكبر من ع  ، قارن بين: س   و   ع

القيمة الأولى أكبر

القيمة الثانية أكبر

القيمتان متساويتان

المعطيات غير كافية

شرح الحل

الحل : (أ).

الفترة رقم 1 : 0:00
سؤال رقم ( 12 )

إذا كان و د يساوي ج د   ،   أ ب = ٤   ،         ب د = ٤ ج د  ،    أوجد مساحة المستطيل ؟

٤٠

٦٤

٨٠

٥٠

شرح الحل

الحل : (ب).

و د = أ ب = ٤  ,  ج د = و د = ٤

ب د = ٤  ج د = ٤ × ٤ = ١٦

أ ب = ٤

المساحة = الطول × العرض = ١٦ × ٤ = ٦٤

الفترة رقم 1 : 0:00
سؤال رقم ( 13 )

مساحة الدائرة ن = ٣٦ ط ، فأوجد مساحة الدائرة م؟

١٤٤ ط

٣٦ ط

١١٢ ط

٢٤ ط

شرح الحل

الحل : (أ).

نق الدائرة ن = ٦

قطر الدائرة ن = ١٢ = نق الدائرة م

مساحة الدائرة م = نق٢ط = ١٤٤ط

الفترة رقم 1 : 0:00
سؤال رقم ( 14 )

فهد يصرف نصف راتبه في أول أسبوع وصرف ٢٠٠٠ في ثاني أسبوع وصرف  right to left 1 over 2 الباقي في ثالث أسبوع فتبقى معه ٥٠٠ ريال في الأسبوع الرابع ، فكم يبلغ راتبه ؟

٣٠٠٠

٤٠٠٠

٥٠٠٠

٦٠٠٠

شرح الحل

الحل : (د).

بتجربة الاختيارات

الفترة رقم 1 : 0:00
سؤال رقم ( 15 )

 إذا كان محيط المستطيل = ٢٨ ، فما هي قيمة س؟

٦

٧

٩

٥

شرح الحل

الحل : (أ).

*بالتجريب*

عند س = ٦ ،  س + ٢ = ٦ + ٢ = ٨

المحيط = (٦ + ٨) × ٢ = ٢٨

الفترة رقم 1 : 0:00
سؤال رقم ( 16 )

قارن بين:  س + ص   و   ١٨٠°

القيمة الأولى أكبر

القيمة الثانية أكبر

القيمتان متساويتان

المعطيات غير كافية

شرح الحل

الحل : (ج).

الفترة رقم 1 : 0:00
سؤال رقم ( 17 )

قارن بين : عددين زوجيين متتاليين   ، عددين فرديين متتاليين

القيمة الأولى أكبر

القيمة الثانية أكبر

القيمتان متساويتان

المعطيات غير كافية

شرح الحل

الحل : (  د )

الفترة رقم 1 : 0:00
سؤال رقم ( 18 )

د ج ينصف زاوية د ، ج قارن بين: قياس الزاوية أ     ،  قياس الزاوية ب

القيمة الأولى أكبر

القيمة الثانية أكبر

القيمتان متساويتان

المعطيات غير كافية

شرح الحل

الحل : ( ج )

المثلث د أ ج و المثلث د ب ج

المثلثان متطابقان لان شروط التطابق تحققت من خلال

الزاوية أ د ج = الزاوية ب أ ج

الزاوية أ ج د = الزاوية ب ج د

وضلع مشترك د ج

من التطابق ينتج أن قياس الزاوية أ = قياس الزاوية ب

الفترة رقم 1 : 0:00
سؤال رقم ( 19 )

في الدائرة م أوجد قيمة س

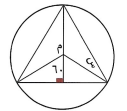
٣٠

٦٠

٤٥

٧٠

شرح الحل

الحل : ( أ )

الفترة رقم 1 : 0:00
سؤال رقم ( 20 )

 اذا كان right to left 5 over س space minus space 2 over 7 space equals space 3 over س   أوجد قيمة س

٣

٤

٦

٧

شرح الحل

الحل : (  د )

الفترة رقم 1 : 0:00
سؤال رقم ( 21 )

اذا كان ٥٪ من عدد ما هو ٢٠ فما قسمة ٥٥٪ منه

٢٢٠

٢٠٠

١٢٠

٢٤٠

شرح الحل

الحل : ( أ )

٥% : ٢٠

٥٥% : س

س = ٢٢٠

الفترة رقم 1 : 0:00
سؤال رقم ( 22 )

اذا كان ن > هـ > ل > صفر قارن بين: right to left ن over ل space space space space space و space space space هـ over ل 

القيمة الأولى أكبر

القيمة الثانية أكبر

القيمتان متساويتان

المعطيات غير كافية

شرح الحل

الحل : ( أ )

ن > هـ  وفي الكسر عندما يتساوى المقامان ننظر للبسط العدد الذي بسطه أكبر يكون هو العدد الأكبر

الفترة رقم 1 : 0:00
سؤال رقم ( 23 )

اذا كان اجمالي عدد الطلاب ١٢٠ فما نسبة طلاب الكيمياء

٢٠%

٢٥% 

٣٠% 

٣٥% 

شرح الحل

الحل : ( ب )

زاوية الكيمياء = ٩٠ درجة و الاحياء = ٩٠ والرياضيات النصف أي ١٨٠ درجة

أي أن الكيمياء الربع أي ٢٥%

الفترة رقم 1 : 0:00
سؤال رقم ( 24 )

أوجد الفرق بين أوروبا والهند

٢٠

١٥

١٠

٥

شرح الحل

الحل : ( ج )

٣٠ – ٢٠ = ١٠

الفترة رقم 1 : 0:00
السؤال اﻷخير

اذا كان اجمالي الفواكه ٥٤٠٠ أوجد مجموع الموز و الخوخ والعنب

٣٢٠٠

٣٢٤٠

٤٠٠٠

٣٨٠٠

شرح الحل

الحل : (  ب )

٥٤٠٠ : ١٠٠%

س : ٦٠%

س = ٣٢٤٠

النتيجة

%

  • عدد اسئلة اﻷختبار 25
  • عدد اﻷجوبة الصحيحة 0
  • عدد اﻷجوبة الخطأ 0